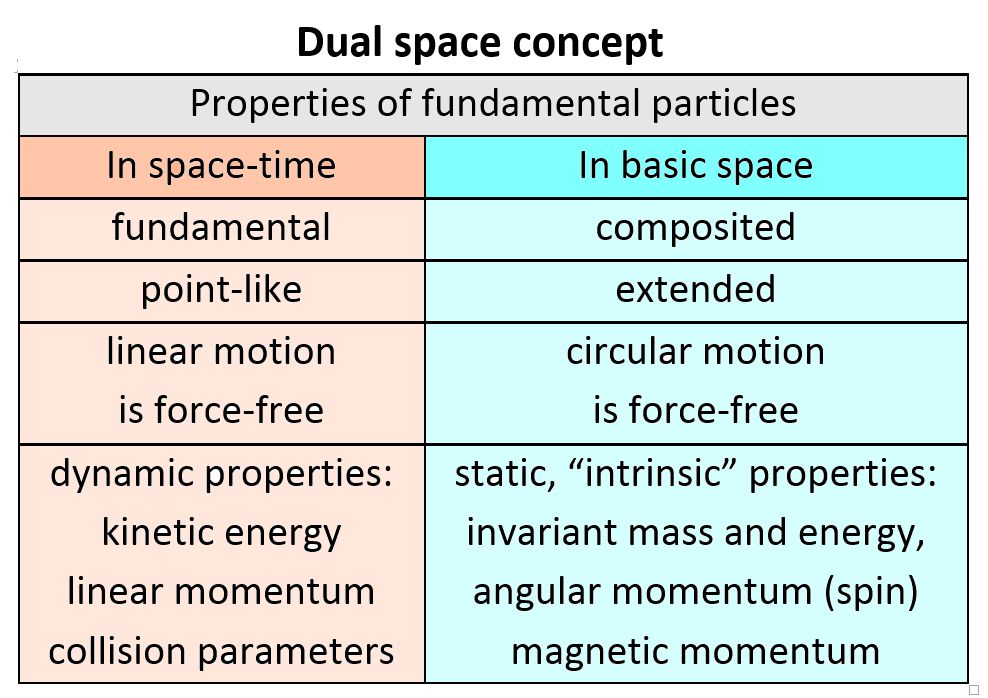
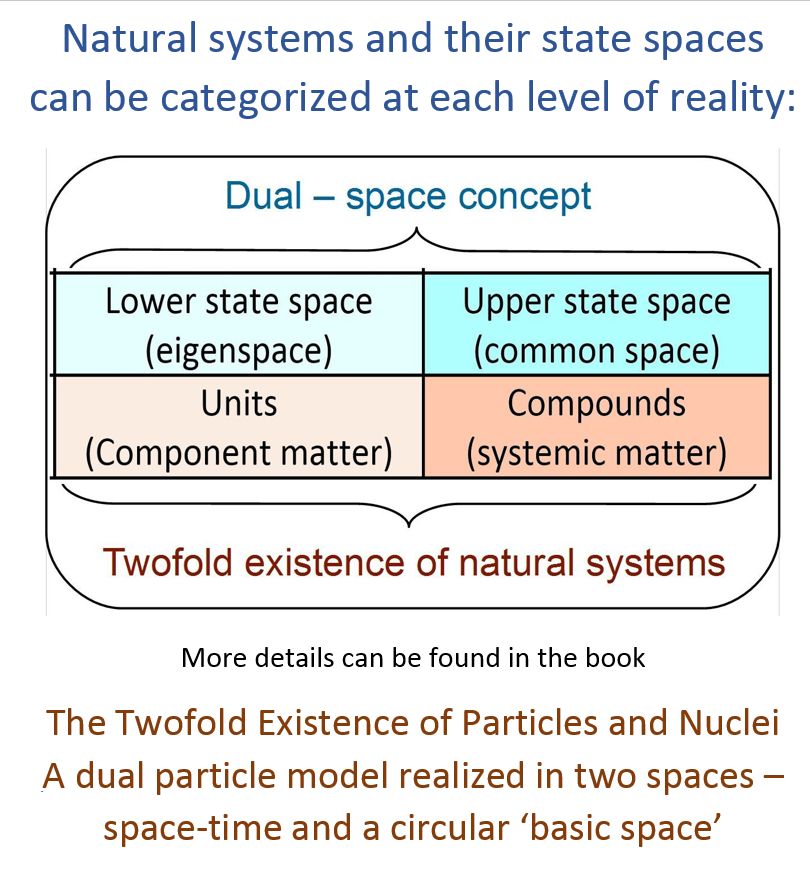
The Dual Space Concept
Welcome to the site of Hans-Dieter Herrmann,
Physicist, Dr. rer.nat.
Physicist, Dr. rer.nat.
Email: Dieter.Herrmann@tonsa.de
Compositeness and spatial extension of fundamental particles
in a circular extra space
(DPG – Conference on Particle Physics Göttingen April 2025)
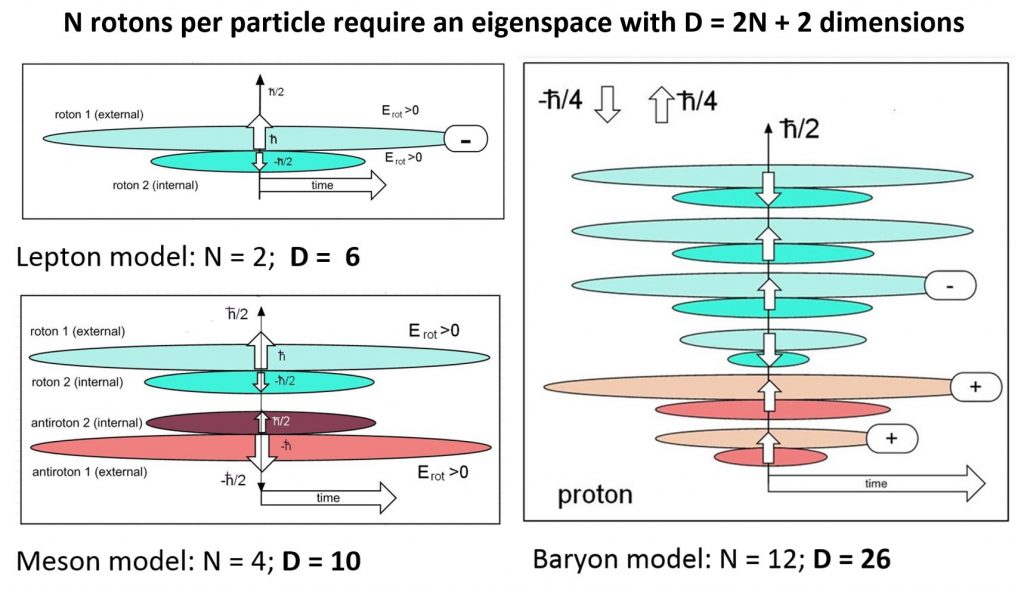
Particle models established in cylindrical eigenspaces
with D = 6, 10 and 26 dimensions
(DPG – Conference on Particle Physics Karlsruhe March 2024)
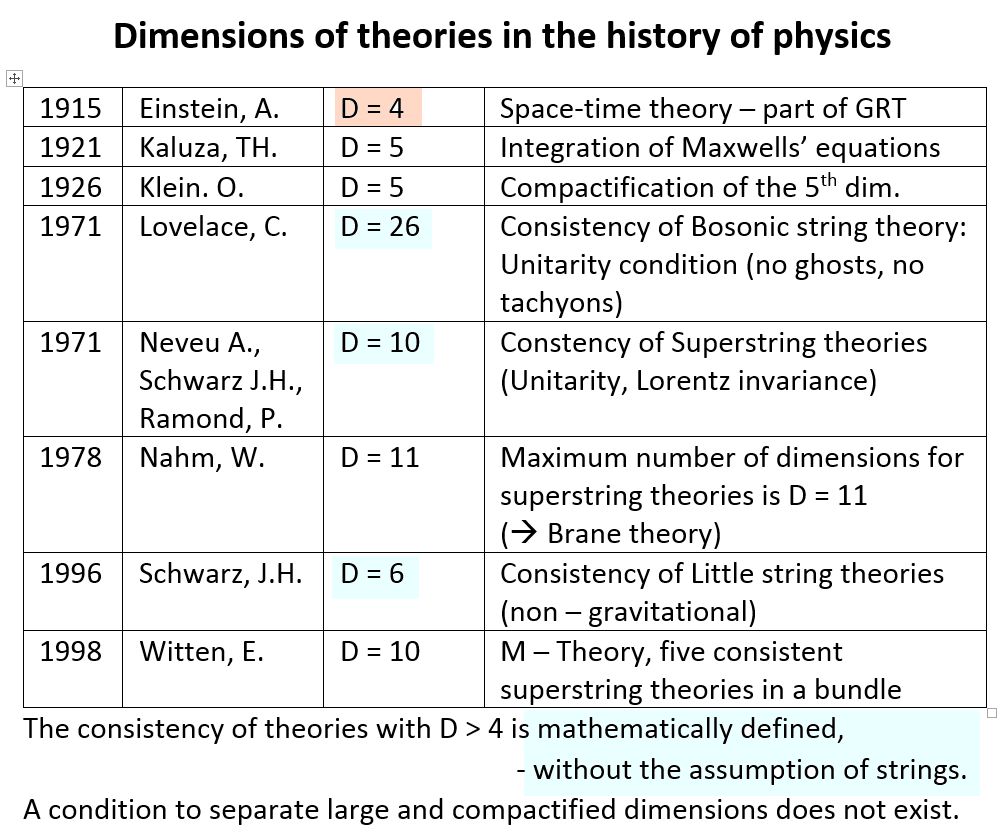
Extra dimensions vs. extra space
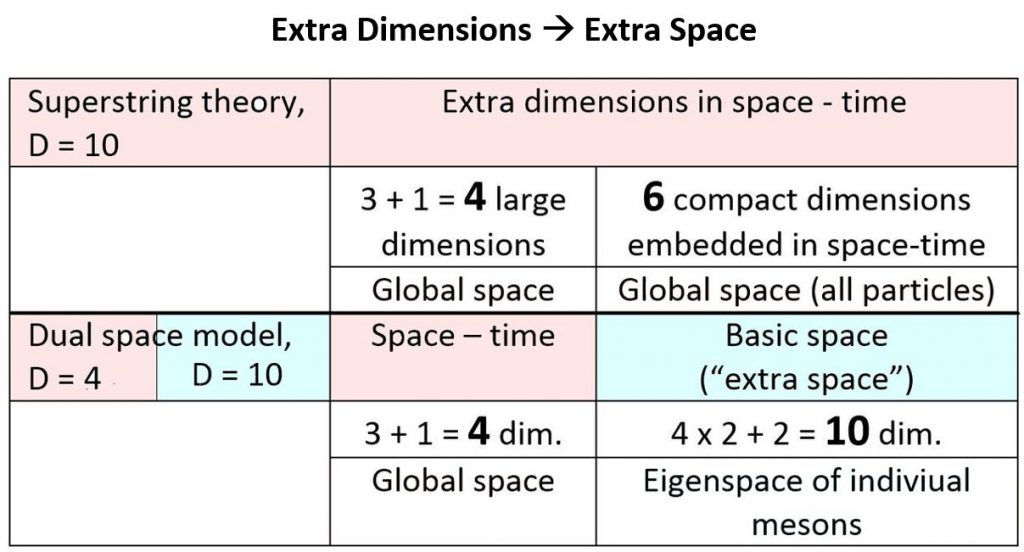
The history of extra dimensions
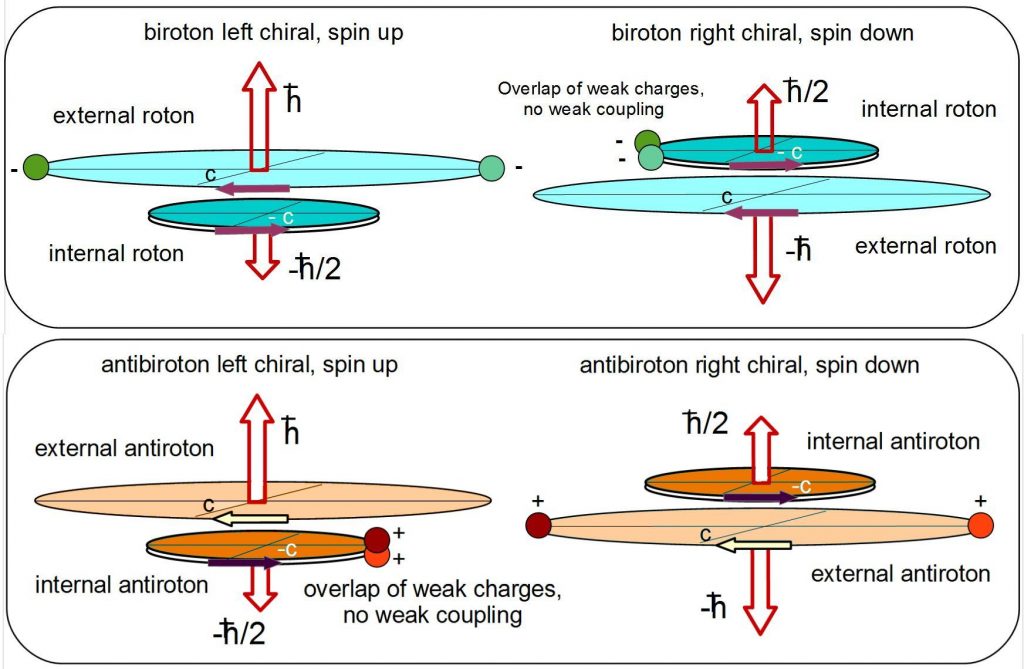
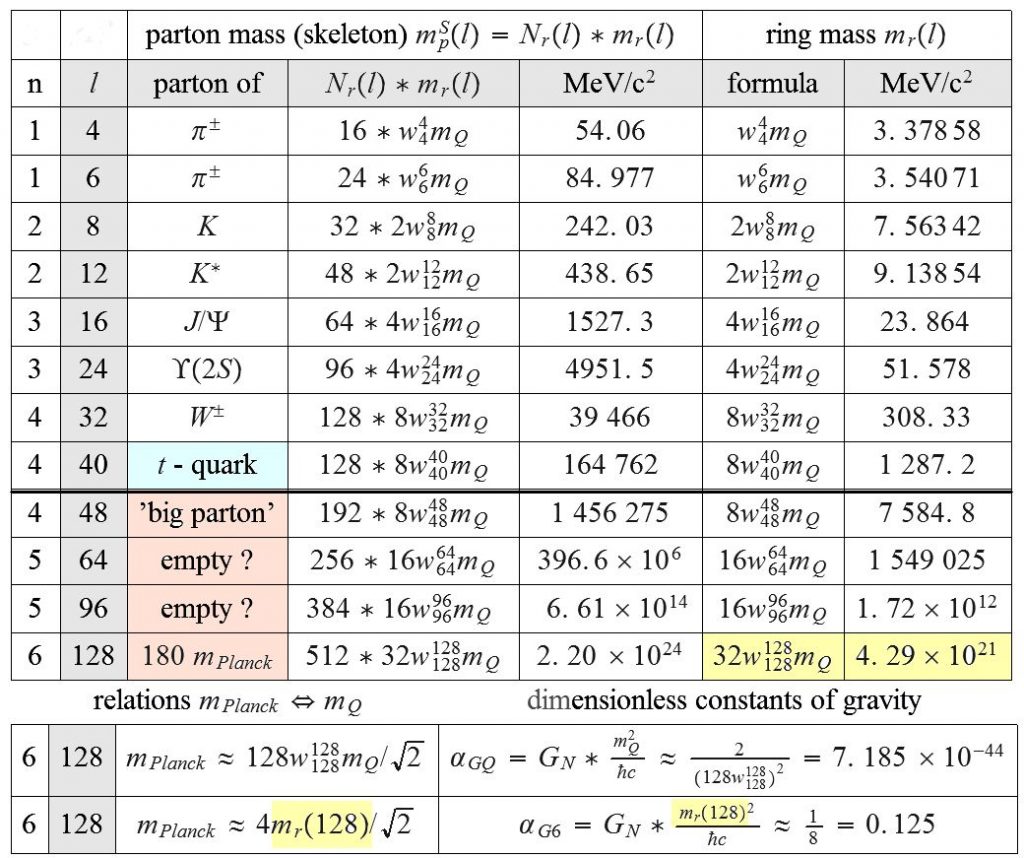
Photon, lepton, meson, baryon models
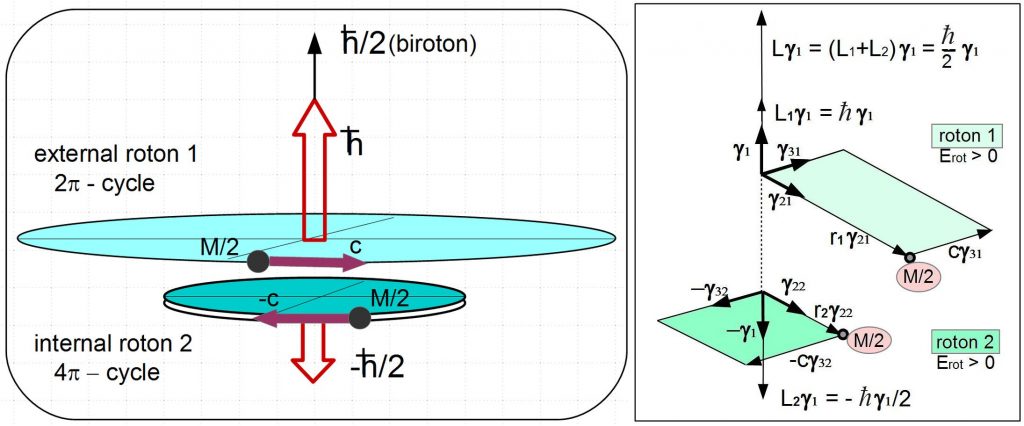
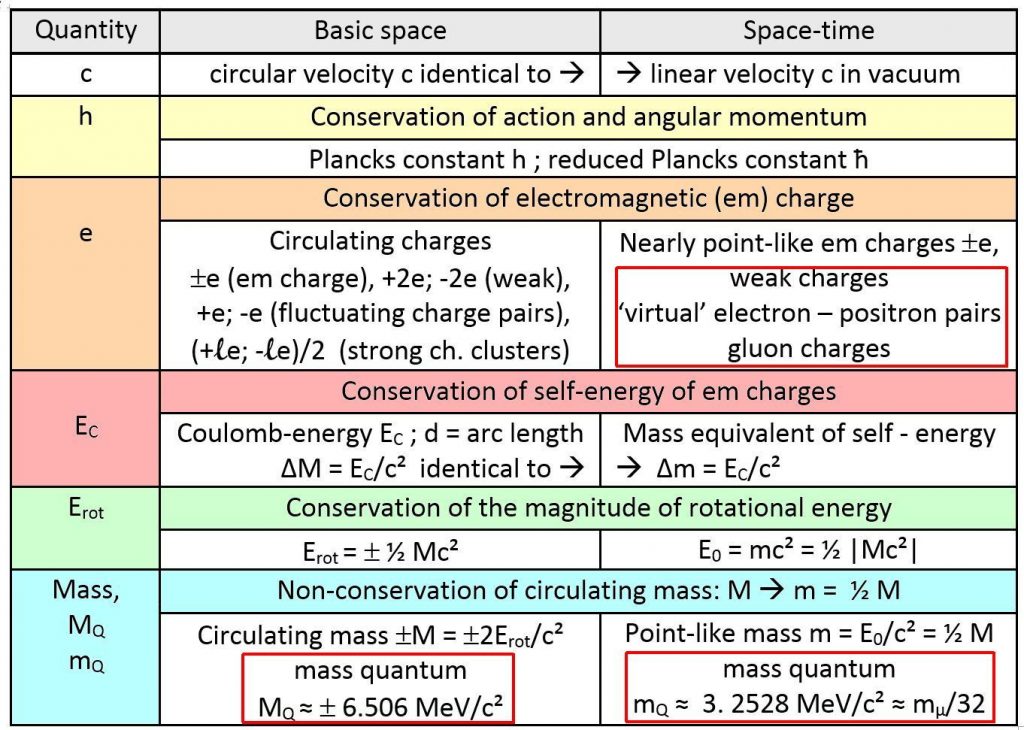
Four fundamental constants

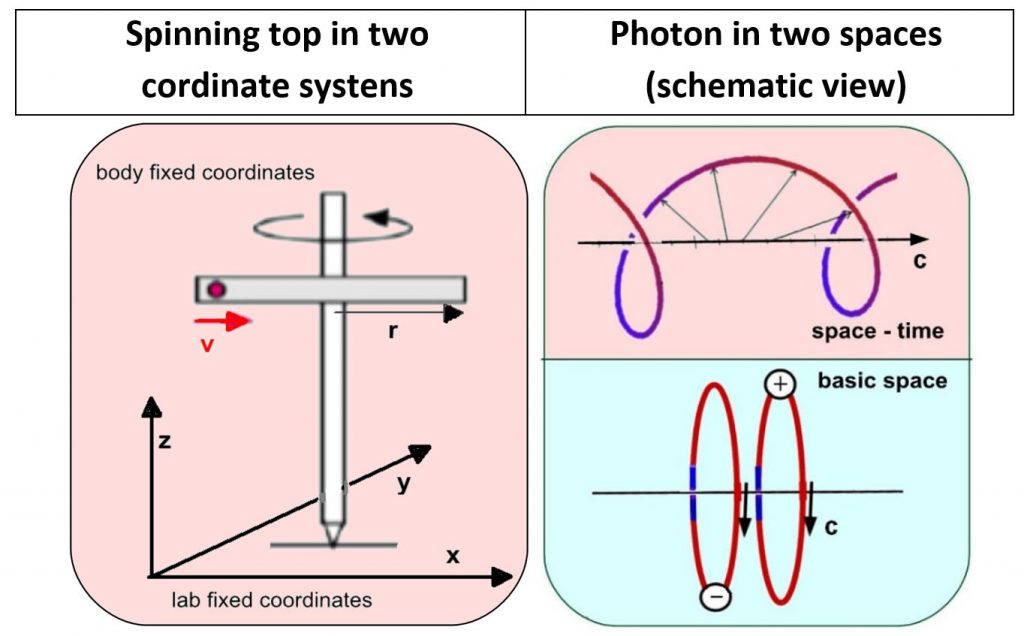
Physical laws in a circular space

Mass generation: Self energy of circulating charges
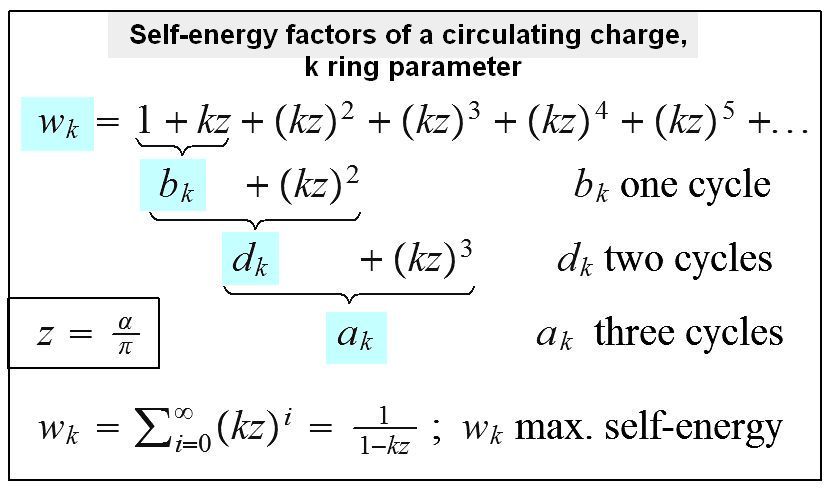
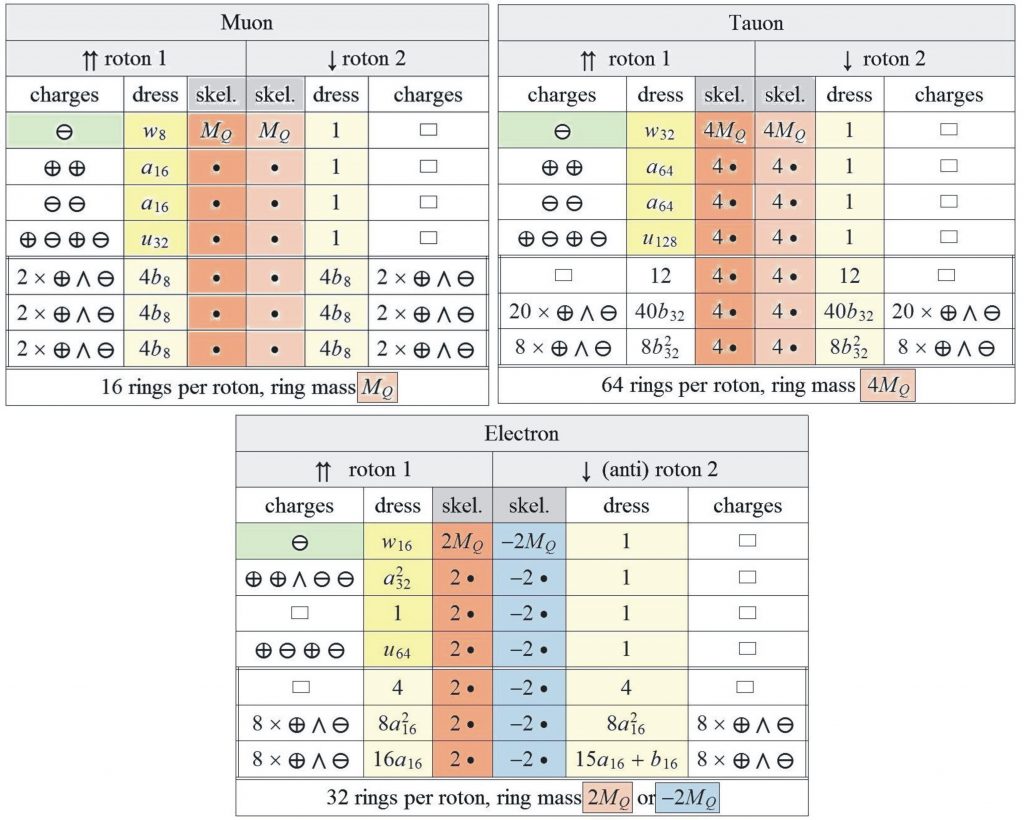

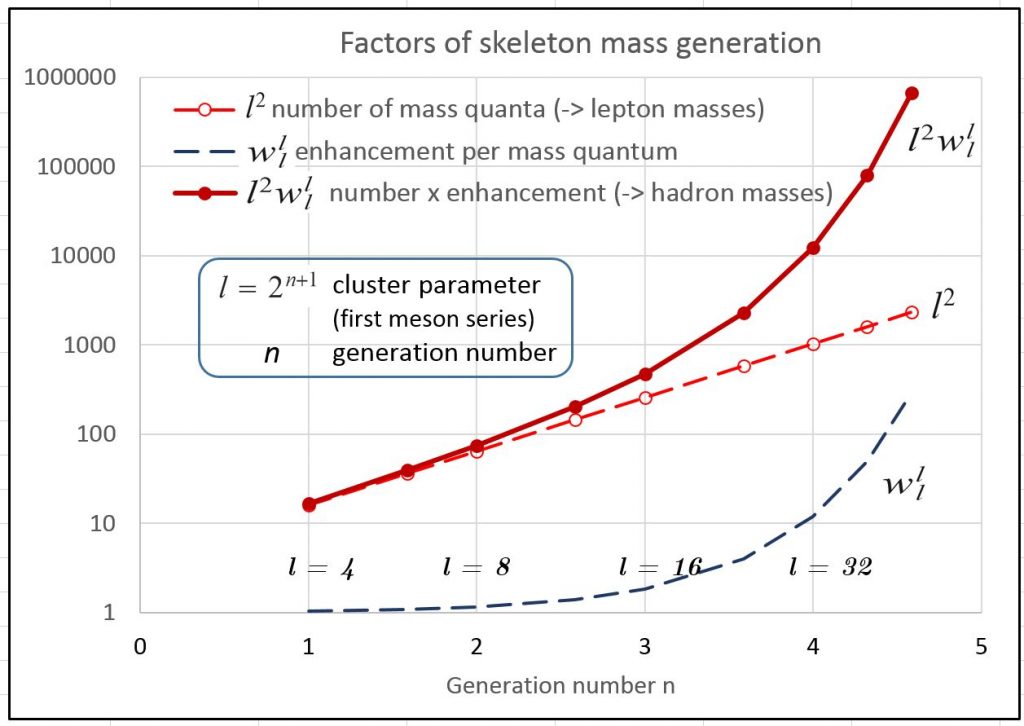
Mass generation: Mass quanta and charge clusters
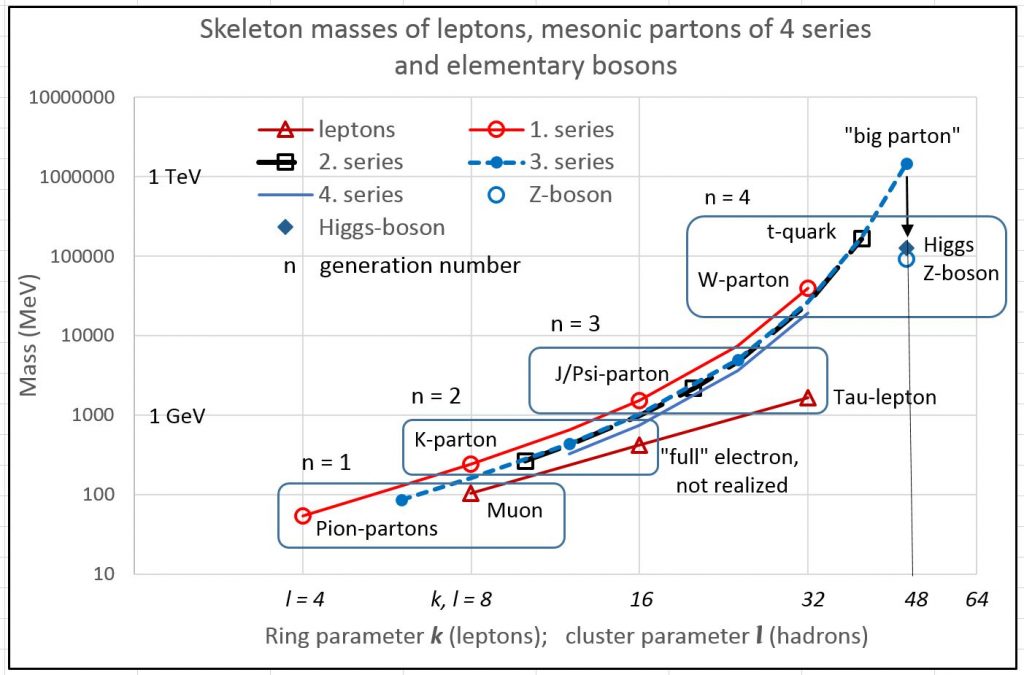
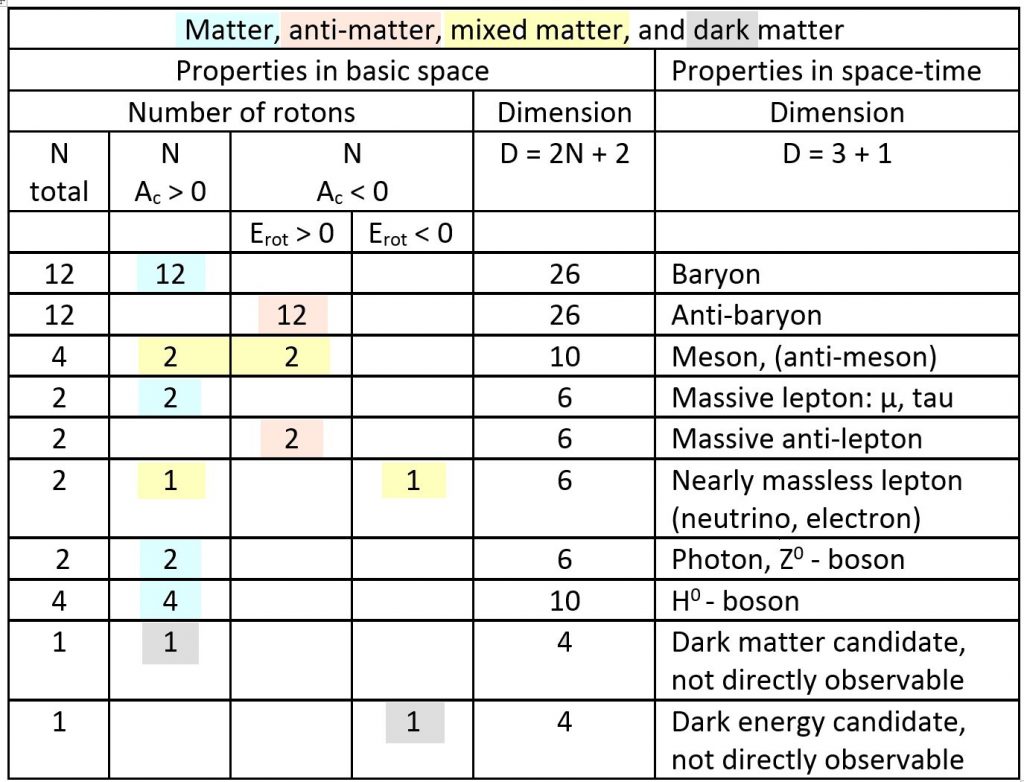
Matter, anti-matter, mixed and dark matter
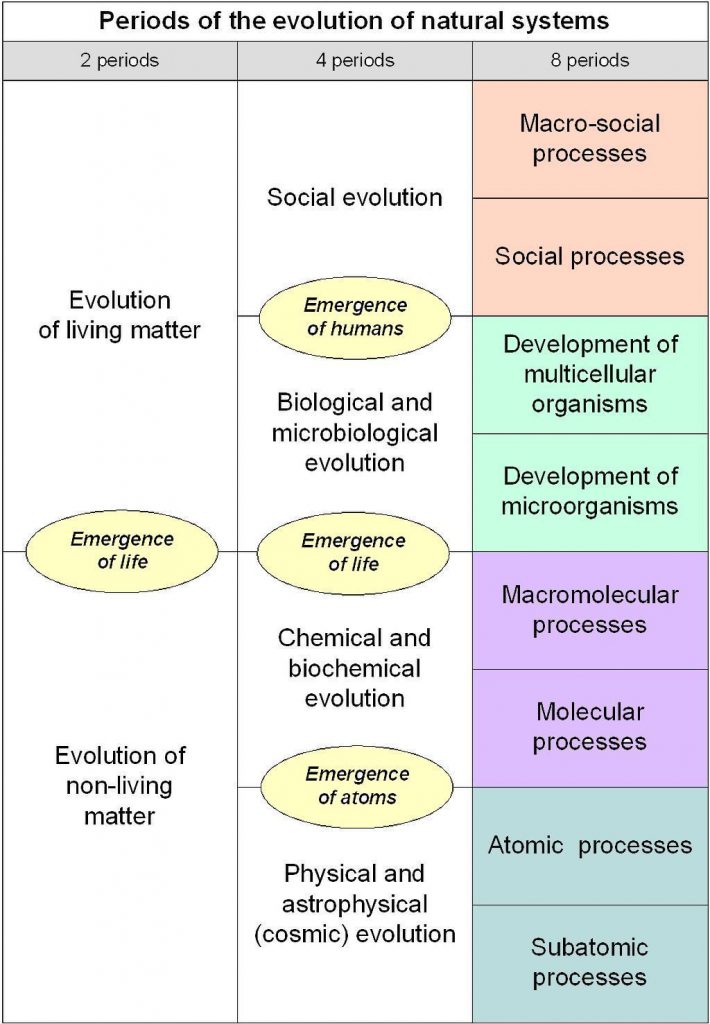
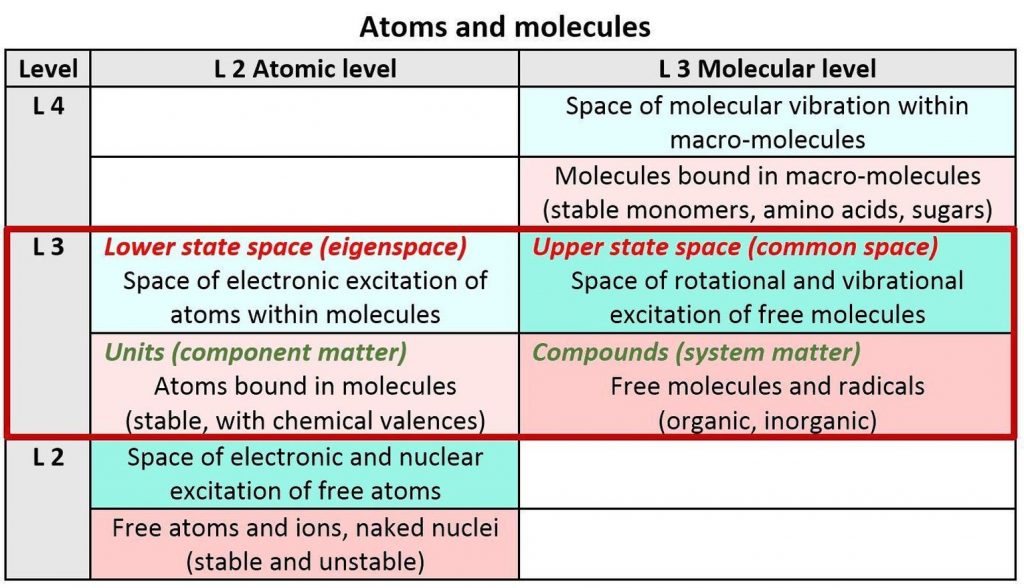
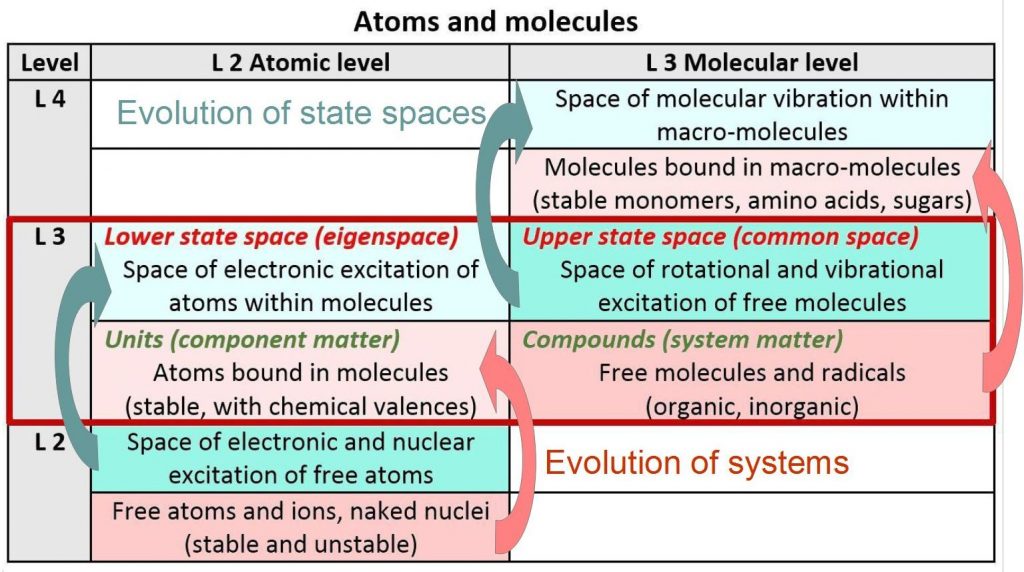
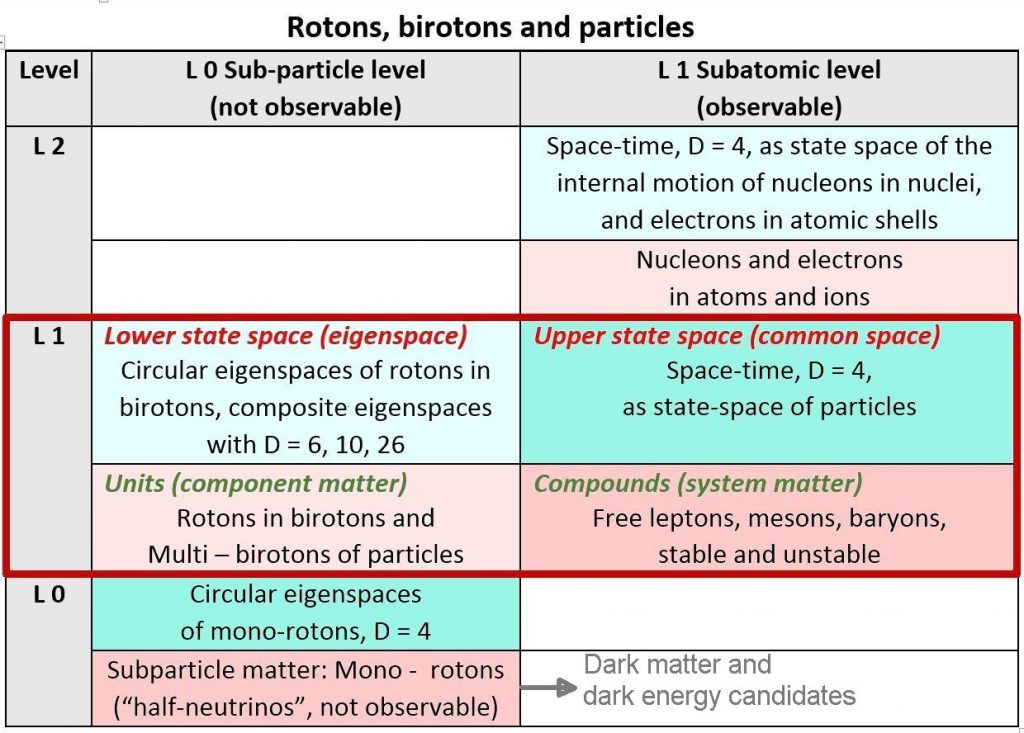
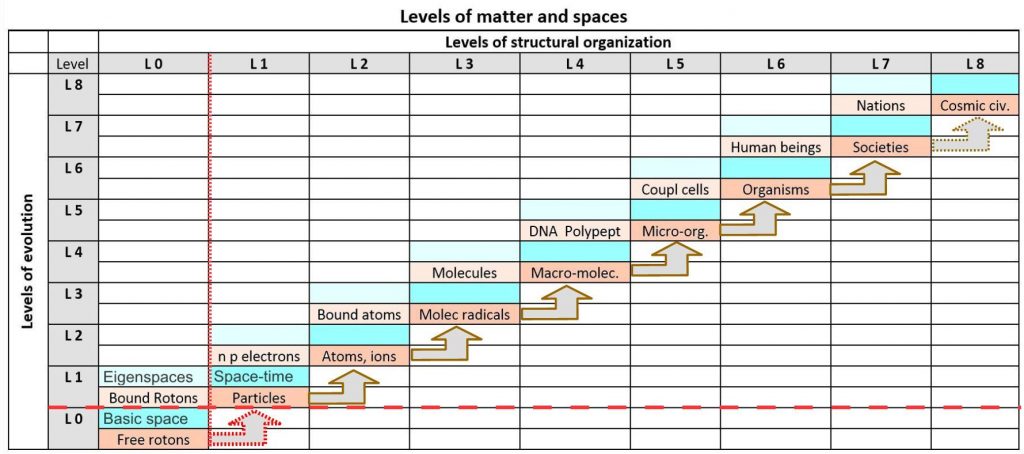
A dual space concept for natural systems at different levels of reality
DPG-Conference on Philosophy of Physics, Bonn 2025
https://www.dpg-verhandlungen.de/year/2025/conference/bonn/part/agphil/session/1/contribution/4?lang=en
DPG – Conference on Philosophy of Physics, Berln 2024
https://www.dpg-verhandlungen.de/year/2024/conference/berlin/part/agphil/session/17/contribution/1
Vertical and horizontal evolution
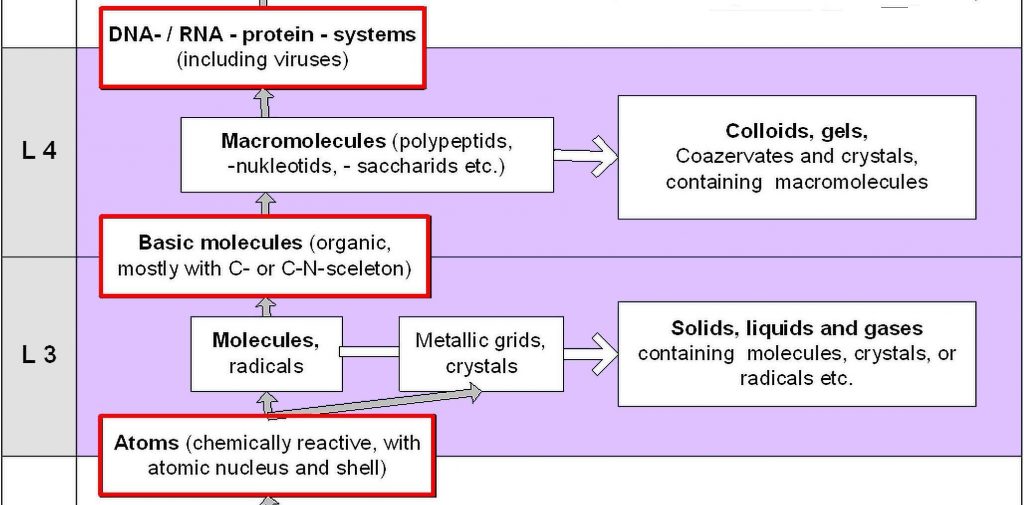
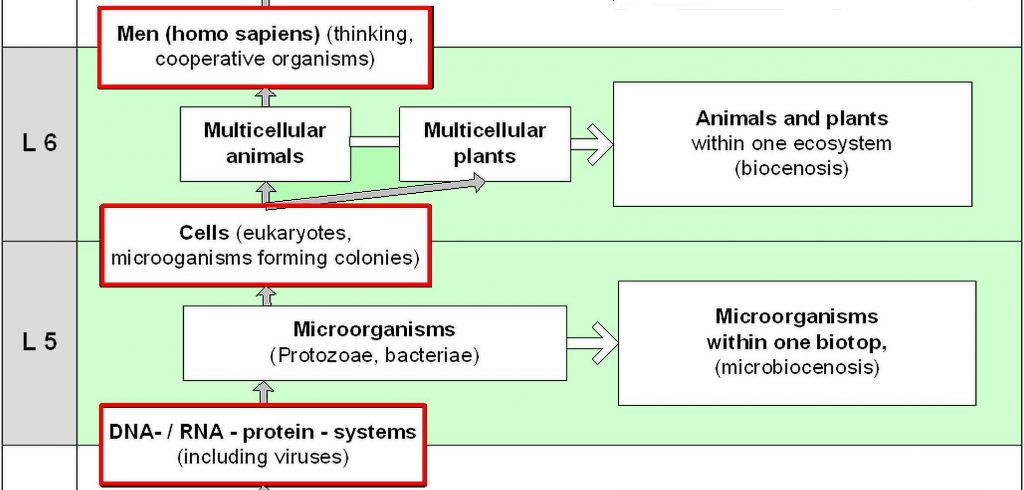
The transition to the next higher level of reality
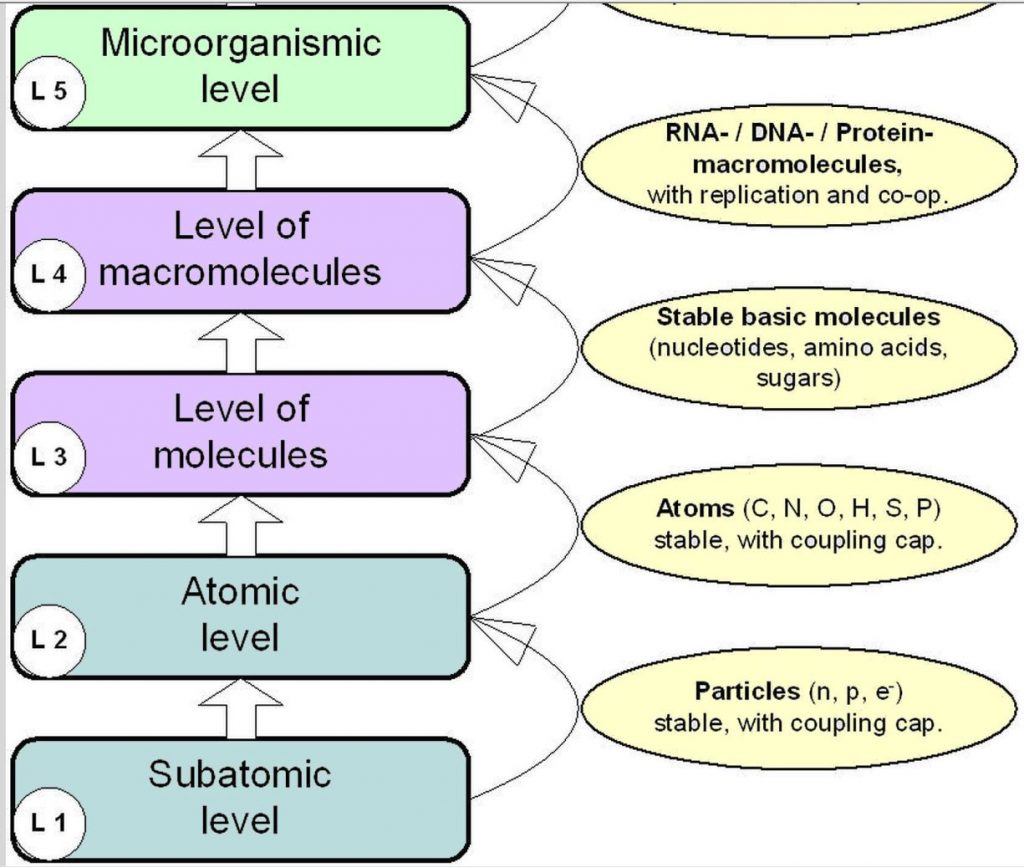
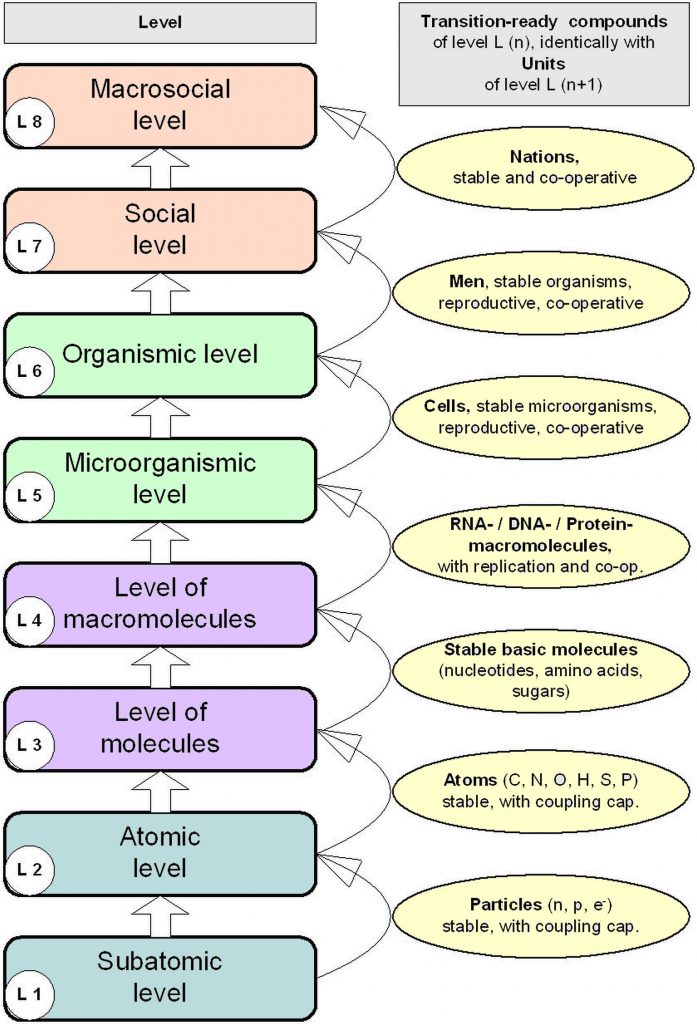
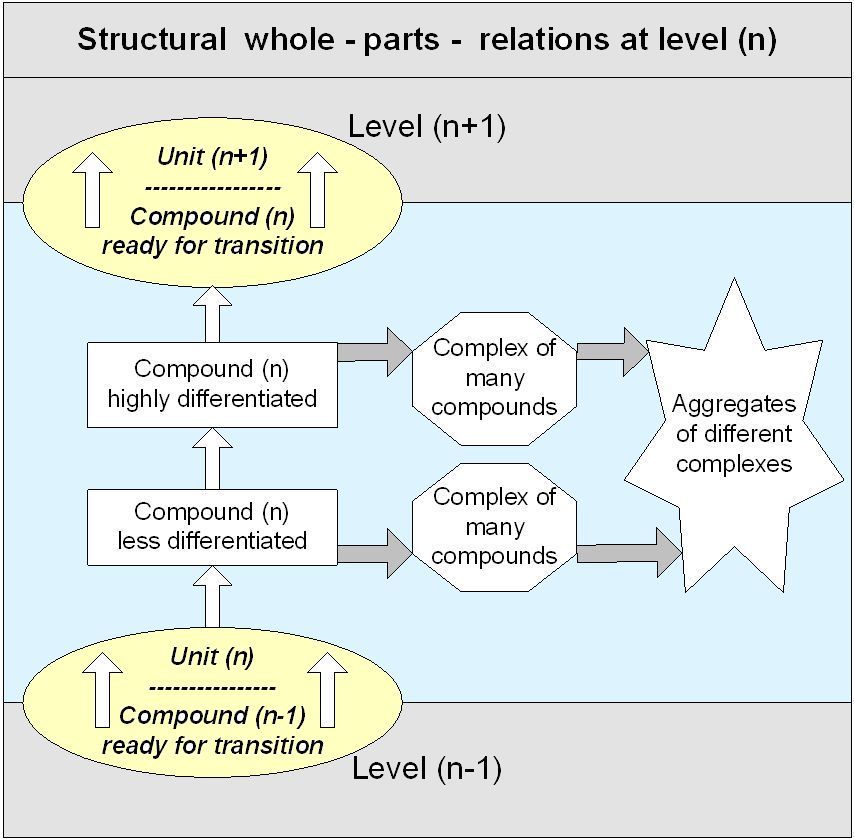
Units and compounds, eigenspaces and common spaces
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.